Steering the Shoggoth: Taming LLMs with Sequential Monte Carlo

The cheese cat sat on
the kitchen counter all day
and dreamed of cheese dreams

In this blog post, we present our findings from an exciting direction in controlling text generation with large language models. We can programmatically define constraints on the output of a model, ensuring it adheres to specific formats or styles, and then can use the Sequential Monte Carlo method to generate samples that satisfy these constraints.

Sequential Monte Carlo steering (or SMC steering), offers some advantages over existing methods:

• Optimized search for possible completions similar to beam search
• Hard constraints (i.e. requiring output to follow a specific grammar)
• Soft constraints (i.e. enforcing a particular writing style)
• A more global approach to constraint satisfaction than techniques like token masking

We will briefly cover the core concepts and potential applications of SMC, and will also present a summary of our experiments with SMC to constrain the length of reasoning traces.

Introduction

Controlling the output of large language models with any degree of certainty remains a significant challenge, even with fine-tuning and reinforcement learning techniques. We found Sequential Monte Carlo Steering of Large Language Models using Probabilistic Programs, a novel framework for constrained language decoding, to be the right fit for addressing this issue. SMC steering offers a powerful approach to constrained language decoding by leveraging the parallel exploration of potential text completions, represented as "particles".

Compared to methods like token masking, which applies constraints locally by filtering tokens at each step, and beam search, which focuses on finding maximum-probability completions, SMC steering approximates a global Bayesian posterior distribution of the output. This enables SMC to satisfy complex constraints while avoiding the pitfalls greedy decoding methods can encounter.

This approach is made possible through the Feynman-Kac Transformer probabilistic model, based on the Feynman-Kac formula. Later on, we will explain how this model enables constraint-driven generation, show how to define both hard and soft constraints, and showcase the power of SMC steering across a handful of tasks.

Sequential Monte Carlo at a Glance

$(s_0, \{M_t\}_{t \geq 1}, \{G_t\}_{t \geq 1})$

• $S_0 \in \mathcal{S}$ The initial state. This starts as an empty string.
• $M_t(s_t | s_{t-1}, f_\theta)$ A Markov kernel (conditional probability) from $s_{t-1}$ to $s_t$, parameterized by the Transformer $f_\theta$.
• $G_t(s_{t-1}, s_t, f_\theta)$ A potential function, assigning a non-negative score to the pair $(s_{t-1}, s_t)$.

The Markov kernel, denoted as $M(s'|s)$ defines a Markov chain that generates text by repeatedly modifying the string $s$ according to probabilistic rules, resulting in a new string $s'$. This process continues until an EOS (end-of-sequence) token is reached, at which point the string stops changing. The potential function, denoted as $G(s)$ assigns scores to states $s$ guiding the generation process toward desired outcomes.

We define a probability distribution that reweights the Markov kernel according to the potential function. The following is adapted from Section 2.1 of the SMC paper.

$$\mathbb{P}_t(s_t) = \frac{\mathbb{E}_M \left[ \prod_{i=1}^{t \wedge T} G_i(S_{i-1}, S_i, f_\theta) \cdot [S_t = s_t] \right]}{\mathbb{E}_M \left[ \prod_{i=1}^{t \wedge T} G_i(S_{i-1}, S_i, f_\theta) \right]}$$
                

$$\mathbb{P}(s) = \lim_{t \rightarrow \infty} \mathbb{P}_t(s)$$
                

With this mathematical foundation established, we can understand how potential functions "filter" the trajectories of the Markov chain, giving higher probability to sequences that better satisfy our constraints. This mathematical framework is what enables SMC to steer language model generation toward desired outcomes while maintaining coherence and quality.

In Code

To define these constraints, the researchers behind SMC developed llamppl, a library that enables stepwise constraints for language decoding using probabilistic programming.

In short, probabilistic programming is a way to build models that include both regular code and elements of randomness. It allows programmers to specify how likely different outcomes are and then perform inference to reason about those probabilities, which goes hand in hand with our goal of constrained language decoding.

From a code perspective, llamppl provides a set of intuitive methods:

• self.condition(bool) This constrains a Boolean expression to be true. It filters out any generation paths that would violate the condition.
• self.observe(dist, val) This samples a value val from a distribution dist and then *forces* the model to act as if it "intended" to generate that specific value.
• self.intervene(dist, val) Similar to observe(), this samples val from dist, but it *doesn't* condition on the sampled value.
• self.sample(dist) This method samples from the given distribution dist, allowing for the model's inherent probabilities to guide the generation.

With just these four methods, you can programmatically define a wide range of constraints, enabling powerful and flexible steering of language models with SMC.

A sample constraint for controlling sentence length:

async def step(self):
    """Generate exactly num_tokens tokens with a coherent sentence ending in period."""
    current_length = len(self.generated_tokens)

    if current_length >= self.num_tokens:
        # Condition on exact length and ending with a period
        self.condition(current_length == self.num_tokens)
        self.condition(self.generated_tokens[-1].token_id in self.period_tokens)
        self.finish()
        return

    next_dist = self.context.next_token()

    if current_length == self.num_tokens - 1:
        # For the last token, force it to be one ending with period
        period_mask = self.period_tokens
        await self.observe(self.context.mask_dist(period_mask), True)
    else:
        # For non-final tokens, prevent period tokens and EOS
        non_period_mask = set(range(len(self.lm.vocab))) - self.period_tokens - {self.lm.tokenizer.eos_token_id}
        await self.observe(self.context.mask_dist(non_period_mask), True)

    # Sample the next token
    token = await self.sample(next_dist)
    self.generated_tokens.append(token)

A Journey Through SMC's Potential

Our initial demos with the SMC framework involved a series of use cases designed to push its capabilities and uncover interesting behaviors, especially around more abstract constraint design and some 'softer' steering targets. Here's a summary of our key exploration areas:

Steering Away from Tokens and Related Concepts

We began by investigating the possibility of steering language model generation away from undesirable words and concepts.

Our approach involved creating a "blocklist" of words (e.g., "car," "vehicle") and then using the model's input embeddings to identify the top 25 most semantically similar tokens. This often produced not only variations of the target words but also related terms (e.g., "truck" for "car") and the target word in other languages.

This could go on and on, and it's fun to observe the model behaviors when incrementally restricting the words it can use

This technique could be very valuable for content moderation, enabling models to generate natural sounding completions while avoiding NSFW or otherwise inappropriate content.

It's worth noting that SMC steering offers a distinct advantage over simple token masking. Instead of just suppressing the probability of certain tokens, SMC aims to generate completions that the model would have produced if it had genuinely "intended" to avoid those words in the first place. See here for an example of the effects of simple token-masking.

Entropy-Based Triggering

Inspired by the efforts behind entropix, we experimented with entropy-based triggering to insertion of a string like "wait..." while generating.

In this setup, we calculated the entropy of the model's next-token predictions at each step. If the entropy exceeded a predefined threshold, we used the observe method to insert a token like "wait..." into the generation sequence, effectively prompting the model to reconsider its trajectory.

The insertion of the "wait..." token here is our soft constraint, with the explicit goal of steering the model towards generation patterns that mimic natural backtracking, where a reasoner might temporarily go down a wrong path before correcting itself.

Control Vector Triggering

We explored the integration of SMC steering with repeng, a project focused on training and inference using control vectors.

While it's technically straightforward to insert a ControlModel (the result of 'wrapping' LLMs to use control vectors in repeng) within the llamppl framework, we observed that this can disrupt SMC's probabilistic nature. Control vectors, by design, alter the LLM's logits or activations, which in turn modifies the probability distribution. This modification violates SMC's assumption that it samples from the inherent distribution of the LLM, leading to unreliable importance weights when resampling particles.

Specifically, direct use of a ControlModel with SMC could push the generation process into mode collapse, resulting in regions of the model's output space far removed from its typical distribution, which would make it difficult for SMC to recover.

To address this issue, we employed a strategy involving two model instances: a standard model and a ControlModel (with the control vector activated), hosted on separate GPUs. We then used the ControlModel's logits as a "proposal distribution" for SMC to steer the base model, where we don't generate directly from the distribution we ultimately care about, but instead, generate from the "proposal" and incorporate the importance weight $( \frac{dist(v)}{proposal(v)} )$ into the potential function. This corrects for the discrepancy between the proposal and the true distribution in the SMC algorithm when using control vectors.

Our "constraint" here is designed with the goal of producing completions where the triggering of the control vector doesn't disrupt the natural flow of language. Instead, the model is encouraged to generate text that reflects the control vector's influence as a deliberate choice within its own generation process.

Length Control

We also investigated the use of SMC for controlling the length of generations, a task that showcases a 'hard' constraint with a clear, objective success measure. Enforcing LLM output to be a coherent sentence of a precise length (e.g., exactly 10, 20, or 150 tokens) is a challenging problem on its own, but with the use of SMC it becomes a simple matter of constraint design (see above code sample for the constraint used here).

Some example completions for different sentence length constraints:

This exploration was motivated by the broader goal of controlling "reasoning length", where we compress the reasoning trace to fit within a target token limit, as detailed below.

A Note on Benchmarking

Initially, benchmarking SMC posed quite the challenge. The llamppl framework's design, which uses a Python library as the primary inference entry point (rather than an API endpoint or HuggingFace weights), makes traditional benchmarking difficult to perform.

Wrapping an API endpoint around a single SMC instance is inefficient because it requires dedicating an entire GPU to store the cached activations for that instance. This necessitates having as many models as available GPUs to maximize inference request processing.

To overcome this, we developed a quick repository to set up a server capable of parallelized SMC inference and experimentation across multiple GPUs. As of 02/19/2025, the llamppl framework was updated to use a vLLM backend (thanks to @benlebrun!), which has greatly improved our ability to conduct efficient benchmarking.

https://github.com/NousResearch/smc-inference-server

Investigating Reasoning Length

Hypothesis

We hypothesized that in reasoning tasks, LLMs might "overthink" or "think past" the correct answer if their reasoning traces are excessively long. In other words, there could be an optimal "Goldilocks" zone for reasoning length – not too short, not too long, just right – that maximizes accuracy.

Experiment Setup

To explore this further, we used the SMC framework and our inference server to evaluate thinking-length constraints with the DeepHermes-3-Llama-3-8B-Preview model. This model was chosen specifically because it provides visibility into the model's reasoning traces, allowing us to analyze the impact of controlling reasoning length on the full MMLU set.

We selected three initial target thinking lengths: 100 tokens, 250 tokens, and 500 tokens. For each target length, we used SMC with 3 particles to approximate reasoning traces. As a reminder, the overall aim here is to constrain the reasoning steps to fit in X number of tokens coherently, meaning that the entire CoT trace fits within that number of tokens.

We acknowledge that inference costs present an obstacle when steering with length-control constraints. The computation involved in re-weighting each particle at step $(t)$ involves revisiting potential function evaluations for all previous steps $(1, 2, ..., t)$, which leads to a linear increase in computational cost per particle with respect to sequence length. In future work, we plan to experiment with similar constraint designs and to benchmark with longer reasoning traces.

Baselines

To provide context for our SMC results, we established the following baselines:

• DeepHermes with no reasoning trace.
• DeepHermes with unconstrained reasoning traces.

We evaluated performance on the full MMLU suite by extracting answers after the reasoning trace using regular expressions, rather than relying on next-token log probabilities for scoring.

For each baseline, we generated 3 responses and used majority voting to determine the final answer. Each of the subsequent SMC benchmarks are run with 3 particles.

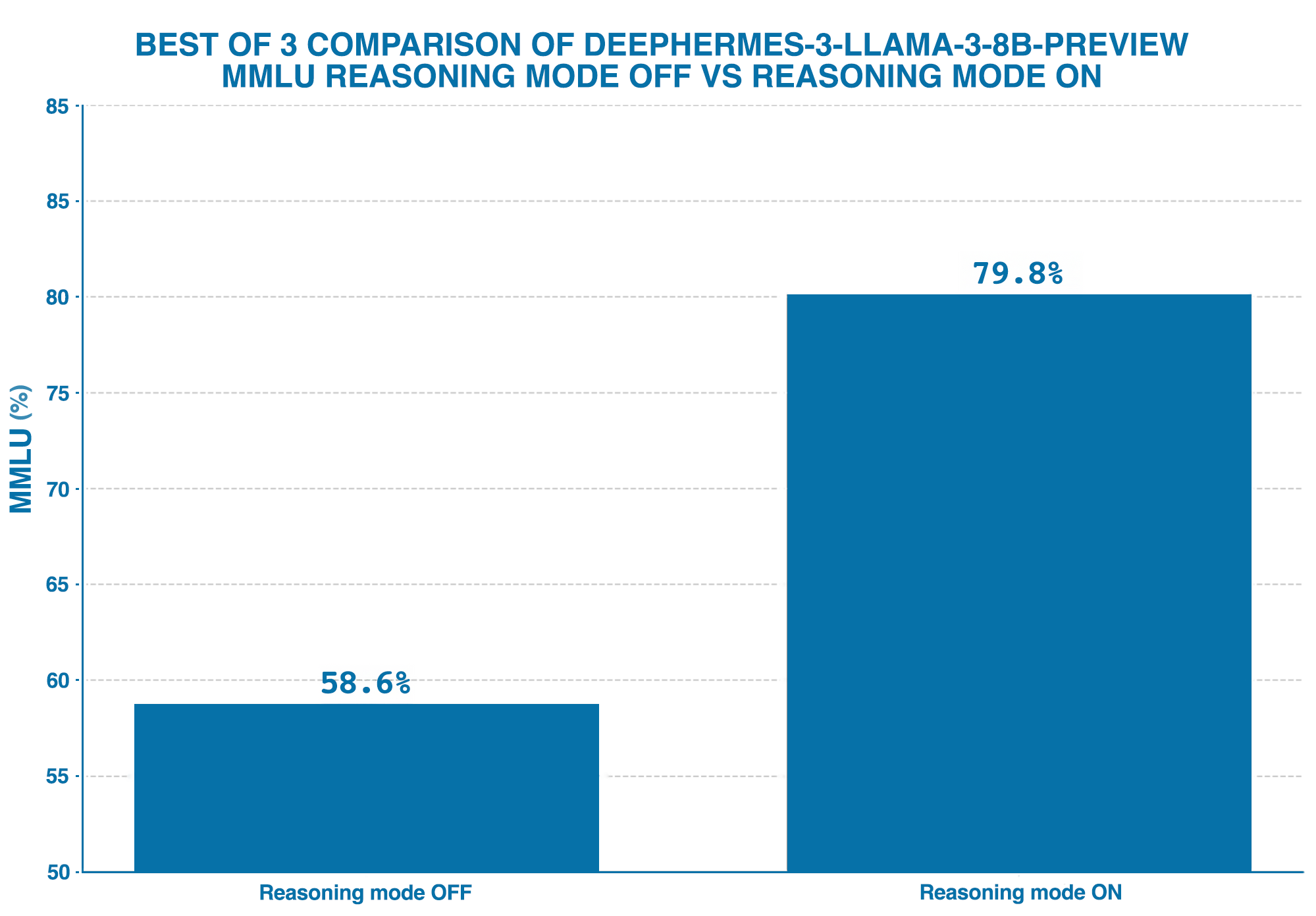
We then tested a simple reasoning length truncation method without SMC. This involved forcing the "end of reasoning" by inserting an end-of-thought token (`</think>`) at token indices 100, 250, and 500 respectively.

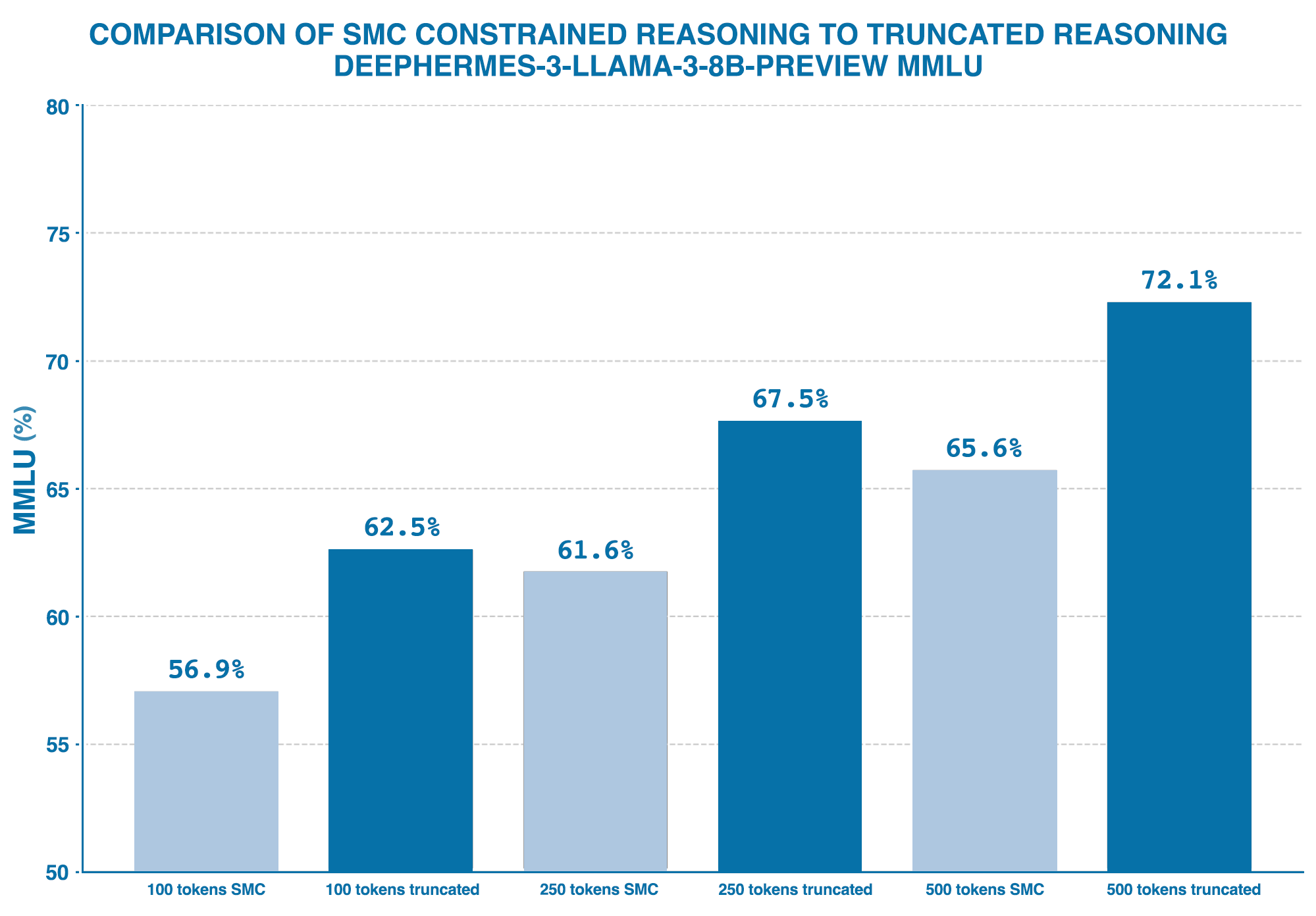
Our results here indicate that simple truncation of the reasoning trace outperforms SMC-constrained reasoning, which aims to generate the entire Chain-of-Thought (CoT) trace within the specified token limit. In contrast, truncation abruptly terminates the CoT generation at exactly 100, 250, or 500 tokens. More detail on this below.

Unpacking the Implications of Reasoning Length Control

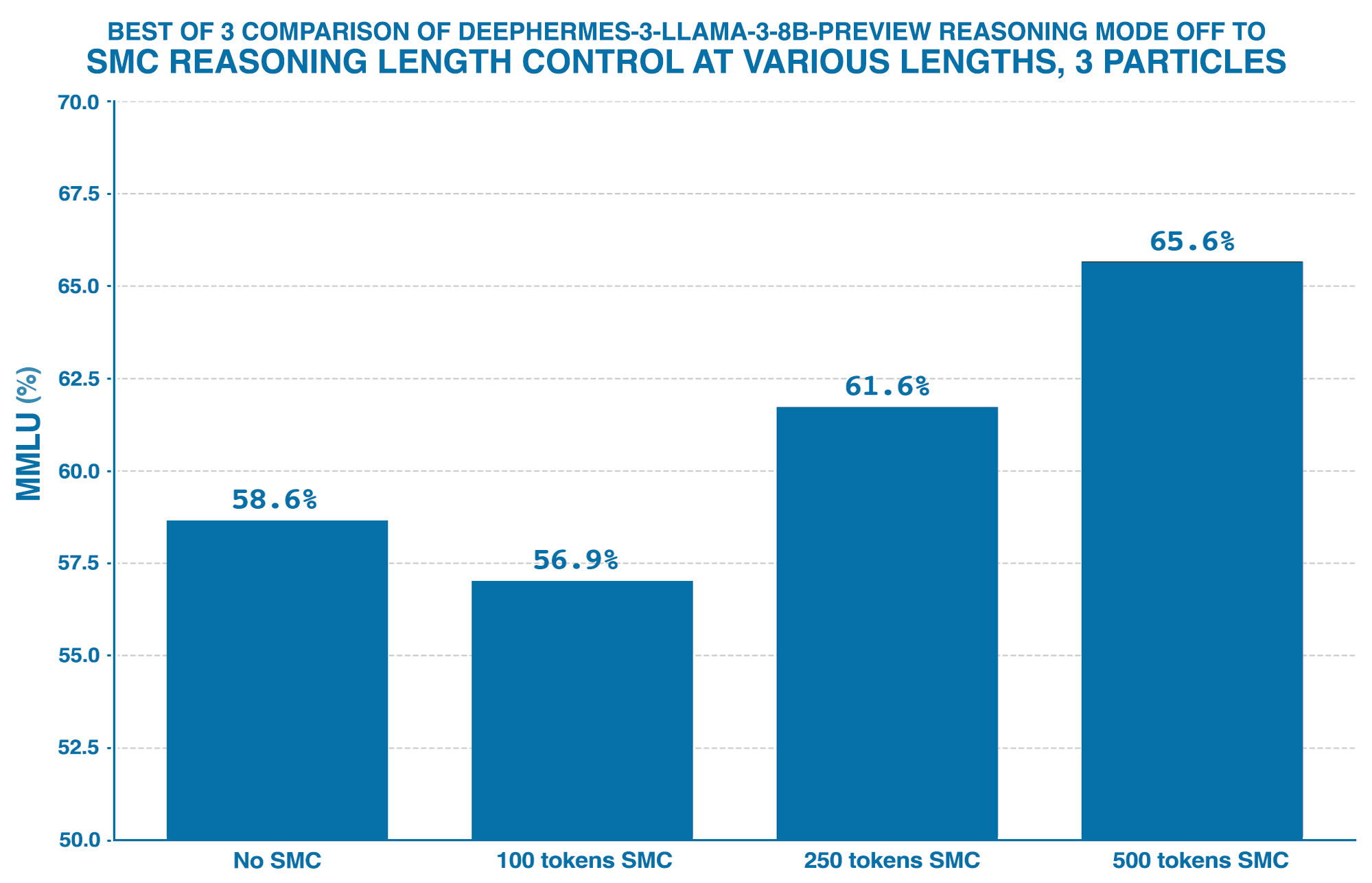
Our experiments yielded several intriguing observations that warrant further discussion:

The "Turing Tape" Analogy: As shown above, we observed a general trend of increasing performance with longer reasoning lengths. This pattern echoes findings from OpenAI regarding the benefits of increased "thinking time" for the o3 model series, reminiscent of the idea that LLMs, given more steps, can better approximate solutions, similar to a Turing tape.

SMC vs. Truncation: A compressed reasoning trace, in comparison to an abrupt interruption of a (likely) much longer reasoning trace, performs worse for all target lengths we tested. Since the latter is reasoning towards a more 'correct' answer on average, without even outputting the actual reasoning tokens, the model might, in some sense, "know" its answer even before fully engaging in the reasoning process. SMC could be steering towards a more 'high-level' or coarse grained reasoning summary.

CoT Faithfulness: This last observation appears to align with emerging research that explores how language models might not be faithful in their reasoning process. Ultimately, the discrepancy between SMC-constrained and truncated reasoning challenges the assumption that Chain-of-Thought traces accurately reflect the model's underlying reasoning process.

We would like to note that the above observations seem contradictory: how could increasing the thinking length linearly improve performance, while truncation of a long CoT performs better than a constrained trace of the same length? Does the reasoning trace matter or not?

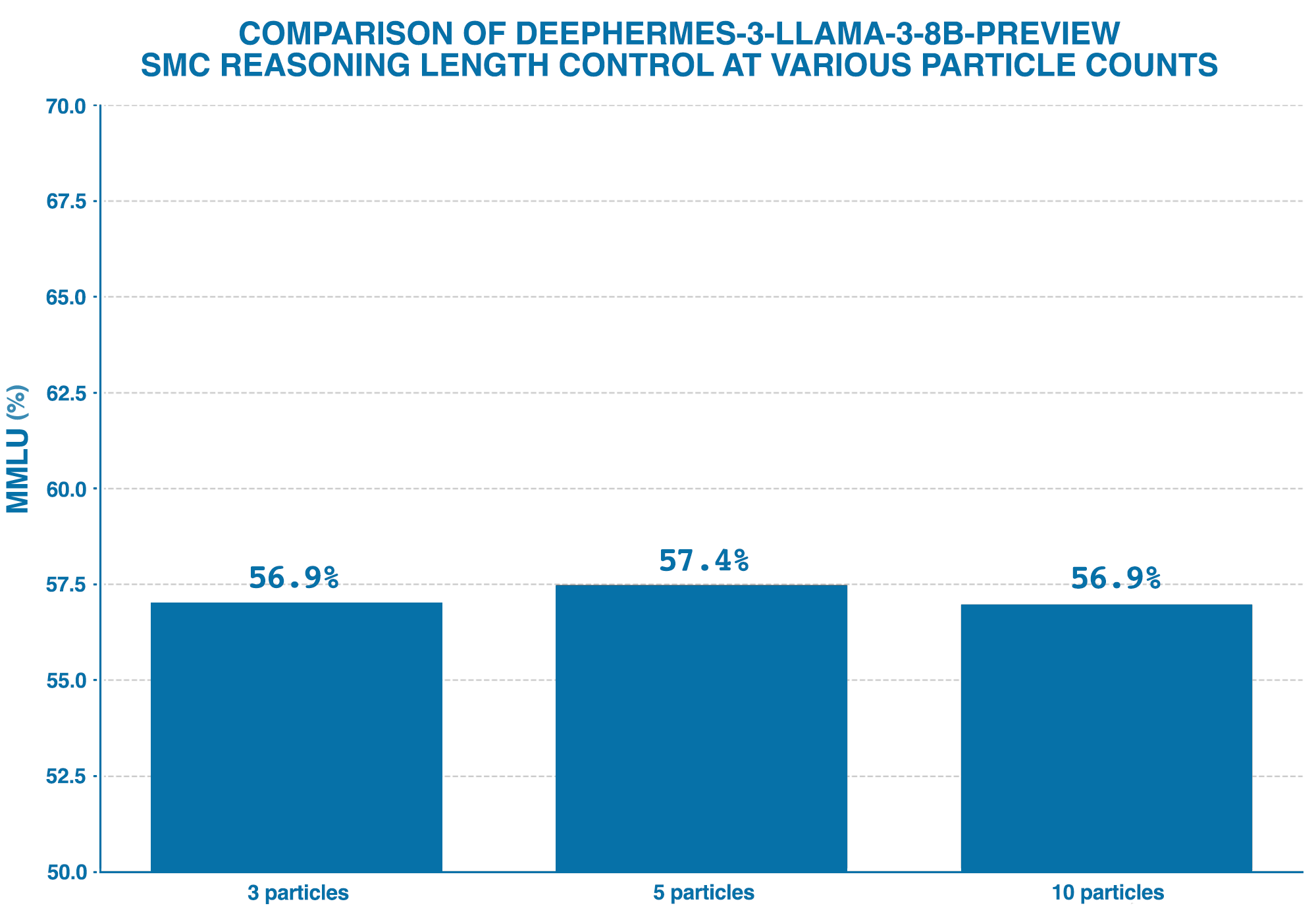
We lastly ran benchmarks for 100 thinking tokens across different particle numbers, to gauge the effectiveness of increasing particle count on our MMLU evaluations. We found that while increasing particle count improves the 'fidelity' of the approximation (of the true posterior), performance increase was barely noticeable. This may be due to our constraint design, and there are likely better alternatives that best define the structure of a compressed thinking trace, but for this experiment we felt this justifies a low particle count for our evaluations.

Charting the Course for Future Steering

This work has illuminated many directions for extending the capabilities of LLM steering. For instance, future research could explore training high-level reasoning control vectors (perhaps with attributes like "pragmatic" or "exploratory") and dynamically triggering them based on high entropy in next-token selection. Benchmarking these techniques on MMLU and other evaluation suites would be a logical next step, given the encouraging preliminary results we've observed with both entropy-based methods and control vector triggering within SMC.

Our long-term vision is to develop with llamppl to produce a general-purpose, extensible steering framework that will enhance LLM performance across diverse domains. The observed impact of various SMC techniques on constrained language decoding reinforces the feasibility of this goal.

Future Work

• Evaluating entropy-based triggering: We have not fully explored the possibilities of entropy-based token insertion, specifically wrt. benchmarks performance. It would be sensible to provide some evaluation on the effectiveness of this technique.
• Prompt intersection: Investigating "multiplayer prompting" scenarios, where multiple users with varying goals interact with the same LLM, could lead to interesting and potentially adversarial dynamics. This is done through proposal distributions or the use of the 'observe' method from different users' distributions.
• Creative writing applications: The unique and sometimes unexpected effects of control vector triggering offer interesting possibilities for creative writing use cases and diverse outputs.

Closing Thoughts

In summary, we've found the SMC framework to be a rich environment for experimentation, and we believe that the ability to achieve guaranteed, constrained language output has large implications, particularly with respect to varying the "scope" of constraints (i.e., soft vs. hard).

We extend our gratitude to the team behind SMC, especially Gabe Grand, whose invaluable contributions made this work possible. We look forward to continued collaboration on future endeavors in the language model steering space.